This lesson is still being designed and assembled (Pre-Alpha version)

previous episode

Introduction to dMRI

next episode

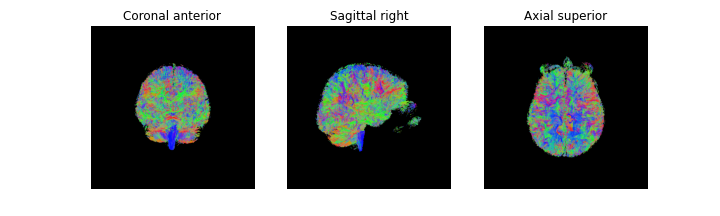
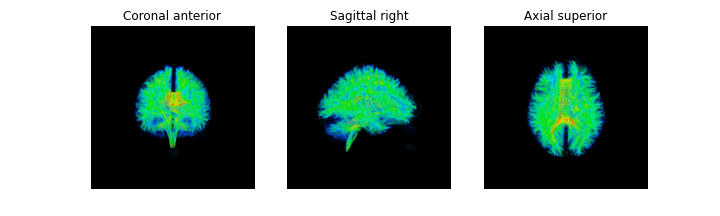
Deterministic tractography

Overview

Teaching: 30 min
Exercises: 0 min
Questions

  • What computations does a deterministic tractography require?

  • How can we visualize the streamlines generated by a tractography method?

Objectives

  • Be able to perform deterministic tracking on diffusion MRI data

  • Familiarize with the data entities of a tractogram

Deterministic tractography

Deterministic tractography algorithms perform tracking of streamlines by following a predictable path, such as following the primary diffusion direction.

In order to demonstrate how to perform deterministic tracking on a diffusion MRI dataset, we will build from the preprocessing presented in a previous episode and compute the diffusion tensor.

import os 

import nibabel as nib
import numpy as np

from bids.layout import BIDSLayout

from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table

dwi_layout = BIDSLayout("../../data/ds000221/derivatives/uncorrected_topup_eddy", validate=False)
gradient_layout = BIDSLayout("../../data/ds000221/", validate=False)

subj = '010006'

dwi_fname = dwi_layout.get(subject=subj, suffix='dwi', extension='.nii.gz', return_type='file')[0]
bvec_fname = dwi_layout.get(subject=subj, extension='.eddy_rotated_bvecs', return_type='file')[0]
bval_fname = gradient_layout.get(subject=subj, suffix='dwi', extension='.bval', return_type='file')[0]

dwi_img = nib.load(dwi_fname)
affine = dwi_img.affine

bvals, bvecs = read_bvals_bvecs(bval_fname, bvec_fname)
gtab = gradient_table(bvals, bvecs)

We will now create a mask and constrain the fitting within the mask.

Tractography run times

Note that many steps in the streamline propagation procedure are computationally intensive, and thus may take a while to complete.

import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu

dwi_data = dwi_img.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)  # Specify the volume index to the b0 volumes

dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask)  # This step may take a while

We will perform tracking using a deterministic algorithm on tensor fields via EuDX (Garyfallidis et al., 2012). EuDX makes use of the primary direction of the diffusion tensor to propagate streamlines from voxel to voxel and a stopping criteria from the fractional anisotropy (FA).

We will first get the FA map and eigenvectors from our tensor fitting. In the background of the FA map, the fitting may not be accurate as all of the measured signal is primarily noise and it is possible that values of NaNs (not a number) may be found in the FA map. We can remove these using numpy to find and set these voxels to 0.

# Create the directory to save the results

out_dir = f"../../data/ds000221/derivatives/dwi/tractography/sub-{subj}/ses-01/dwi/"

if not os.path.exists(out_dir):
    os.makedirs(out_dir)

fa_img = dti_fit.fa
evecs_img = dti_fit.evecs

fa_img[np.isnan(fa_img)] = 0

# Save the FA
fa_nii = nib.Nifti1Image(fa_img.astype(np.float32), affine)
nib.save(fa_nii, os.path.join(out_dir, 'fa.nii.gz'))

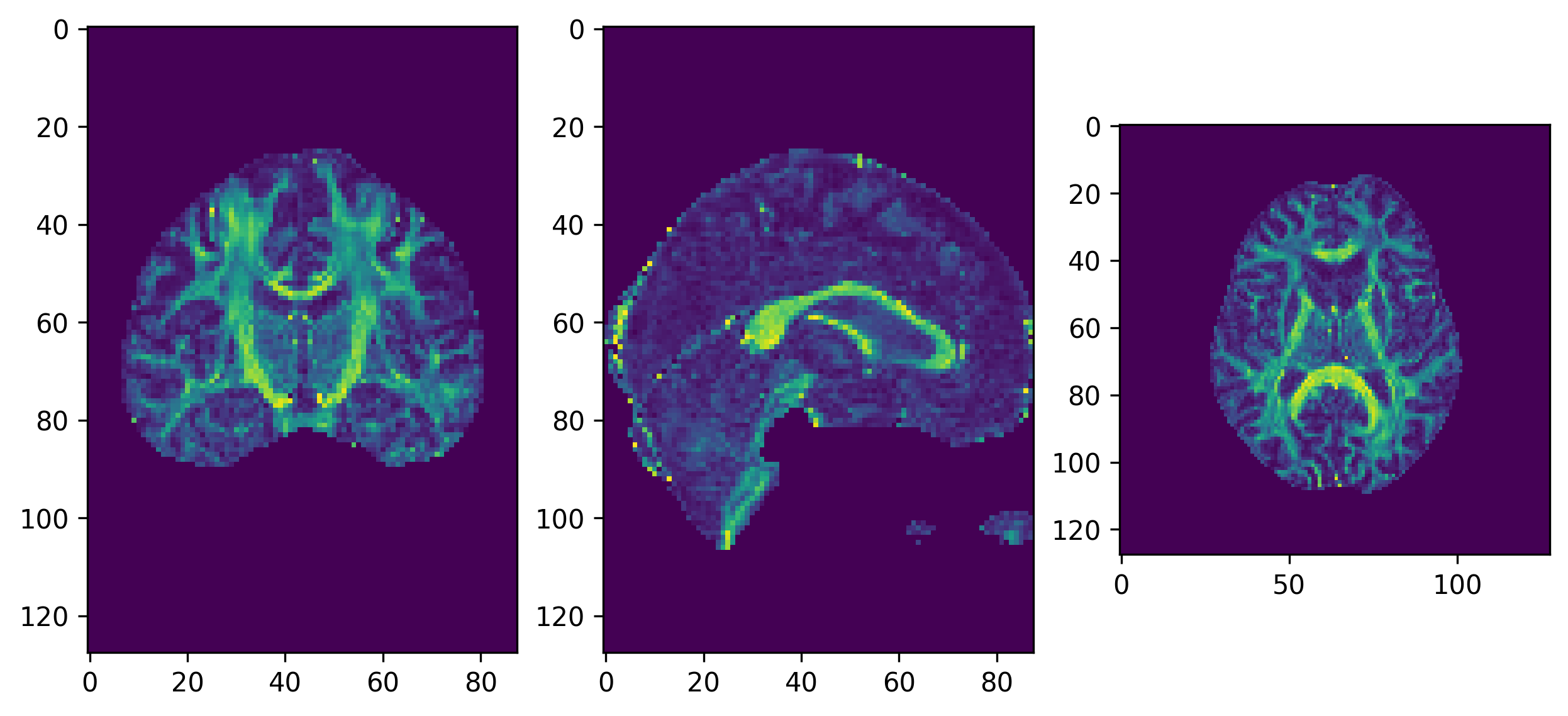
# Plot the FA
import matplotlib.pyplot as plt
from scipy import ndimage  # To rotate image for visualization purposes

%matplotlib inline

fig, ax = plt.subplots(1, 3, figsize=(10, 10))
ax[0].imshow(ndimage.rotate(fa_img[:, fa_img.shape[1]//2, :], 90, reshape=False))
ax[1].imshow(ndimage.rotate(fa_img[fa_img.shape[0]//2, :, :], 90, reshape=False))
ax[2].imshow(ndimage.rotate(fa_img[:, :, fa_img.shape[-1]//2], 90, reshape=False))
fig.savefig(os.path.join(out_dir, "fa.png"), dpi=300, bbox_inches="tight")
plt.show()

FA

One of the inputs of EuDX is the discretized voxel directions on a unit sphere. Therefore, it is necessary to discretize the eigenvectors before providing them to EuDX. We will use an evenly distributed sphere of 362 points using the get_sphere function.

from dipy.data import get_sphere

sphere = get_sphere('symmetric362')

We will determine the indices representing the discretized directions of the peaks by providing as input, our tensor model, the diffusion data, the sphere, and a mask to apply the processing to. Additionally, we will set the minimum angle between directions, the maximum number of peaks to return (1 for the tensor model), and the relative peak threshold (returning peaks greater than this value).

from dipy.direction import peaks_from_model

peak_indices = peaks_from_model(
    model=dti_model, data=dwi_data, sphere=sphere, relative_peak_threshold=.2,
    min_separation_angle=25, mask=dwi_mask, npeaks=2)

Additionally, we will apply a stopping criterion for our tracking based on the FA map. That is, we will stop our tracking when we reach a voxel where FA is below 0.2.

from dipy.tracking.stopping_criterion import ThresholdStoppingCriterion

stopping_criterion = ThresholdStoppingCriterion(fa_img, .2)

We will also need to specify where to “seed” (begin) the fiber tracking. Generally, the seeds chosen will depend on the pathways one is interested in modelling. In this example, we will create a seed mask from the FA map thresholding above our stopping criterion.

from dipy.tracking import utils

seed_mask = fa_img.copy()
seed_mask[seed_mask >= 0.2] = 1
seed_mask[seed_mask < 0.2] = 0

seeds = utils.seeds_from_mask(seed_mask, affine=affine, density=1)

Now, we can apply the tracking algorithm!

As mentioned previously, EuDX is the fiber tracking algorithm that we will be using. The most important parameters to include are the indices representing the discretized directions of the peaks (peak_indices), the stopping criterion, the seeds, the affine transformation, and the step sizes to take when tracking!

from dipy.tracking.local_tracking import LocalTracking
from dipy.tracking.streamline import Streamlines

# Initialize local tracking - computation happens in the next step.
streamlines_generator = LocalTracking(
    peak_indices, stopping_criterion, seeds, affine=affine, step_size=.5)

# Generate streamlines object
streamlines = Streamlines(streamlines_generator)

We just created a deterministic set of streamlines using the EuDX algorithm mapping the human brain connectome (tractography). We can save the streamlines as a Trackvis file so it can be loaded into other software for visualization or further analysis. To do so, we need to save the tractogram state using StatefulTractogram and save_tractogram to save the file. Note that we will have to specify the space to save the tractogram in.

from dipy.io.stateful_tractogram import Space, StatefulTractogram
from dipy.io.streamline import save_tractogram

sft = StatefulTractogram(streamlines, dwi_img, Space.RASMM)

# Save the tractogram
save_tractogram(sft, os.path.join(out_dir, "tractogram_deterministic_EuDX.trk"))

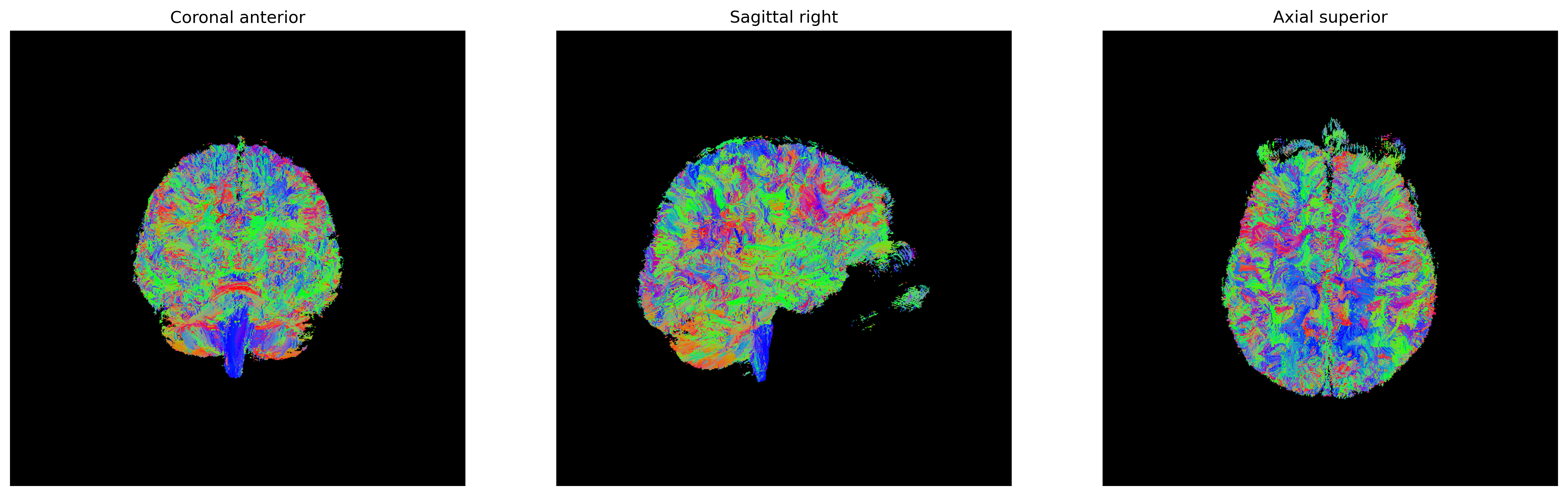
We can then generate the streamlines 3D scene using the FURY python package, and visualize the scene’s contents with Matplotlib.

from fury import actor, colormap

from utils.visualization_utils import generate_anatomical_volume_figure

# Plot the tractogram

# Build the representation of the data
streamlines_actor = actor.line(streamlines, colormap.line_colors(streamlines))

# Generate the figure
fig = generate_anatomical_volume_figure(streamlines_actor)

fig.savefig(os.path.join(out_dir, "tractogram_deterministic_EuDX.png"),
            dpi=300, bbox_inches="tight")
plt.show()

EuDX Determinsitic Tractography

Exercise 1

In this episode, we applied a threshold stopping criteria to stop tracking when we reach a voxel where FA is below 0.2. There are also other stopping criteria available. We encourage you to read the DIPY documentation about the others. For this exercise, repeat the tractography, but apply a binary stopping criteria (BinaryStoppingCriterion) using the seed mask. Visualize the tractogram!

Solution

import os

import nibabel as nib
import numpy as np

from bids.layout import BIDSLayout

from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
from dipy.data import get_sphere
from dipy.direction import peaks_from_model
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
from dipy.tracking import utils
from dipy.tracking.local_tracking import LocalTracking
from dipy.tracking.streamline import Streamlines

from utils.visualization_utils import generate_anatomical_volume_figure
from fury import actor, colormap
import matplotlib.pyplot as plt

dwi_layout = BIDSLayout("../../data/ds000221/derivatives/uncorrected_topup_eddy", validate=False)
gradient_layout = BIDSLayout("../../data/ds000221/", > > validate=False)

# Get subject data
subj = '010006'
dwi_fname = dwi_layout.get(subject=subj, suffix='dwi', extension='.nii.gz', return_type='file')[0]
bvec_fname = dwi_layout.get(subject=subj, extension='.eddy_rotated_bvecs', return_type='file')[0]
bval_fname = gradient_layout.get(subject=subj, suffix='dwi', extension='.bval', return_type='file')[0]

dwi_img = nib.load(dwi_fname)
affine = dwi_img.affine

bvals, bvecs = read_bvals_bvecs(bval_fname, bvec_fname)
gtab = gradient_table(bvals, bvecs)

dwi_data = dwi_img.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)  # Specify the volume index to the b0 volumes

# Fit tensor and compute FA map
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask)  
fa_img = dti_fit.fa
evecs_img = dti_fit.evecs

sphere = get_sphere('symmetric362')
peak_indices = peaks_from_model(
       model=dti_model, data=dwi_data, sphere=sphere,
       relative_peak_threshold=.2, min_separation_angle=25, mask=dwi_mask,
       npeaks=2)

# Create a binary seed mask
seed_mask = fa_img.copy()
seed_mask[seed_mask >= 0.2] = 1
seed_mask[seed_mask < 0.2] = 0

seeds = utils.seeds_from_mask(seed_mask, affine=affine, density=1)

# Set stopping criteria
stopping_criterion = BinaryStoppingCriterion(seed_mask==1)

# Perform tracking
streamlines_generator = LocalTracking(
    peak_indices, stopping_criterion, seeds, affine=affine, step_size=.5)
streamlines = Streamlines(streamlines_generator)

# Plot the tractogram
# Build the representation of the data
streamlines_actor = actor.line(streamlines, colormap.line_colors(streamlines))

# Generate the figure
fig = generate_anatomical_volume_figure(streamlines_actor)
plt.show()

Binary Stopping Criterion Tractography

Exercise 2

As an additional challenge, set the color of the streamlines to display the values of the FA map and change the opacity to 0.05. You may need to transform the streamlines from world coordinates to the subject’s native space using transform_streamlines from dipy.tracking.streamline.

Solution

import numpy as np
from fury import actor

from dipy.tracking.streamline import transform_streamlines
from utils.visualizations_utils import generate_anatomical_volume_figure
import matplotlib.pyplot as plt 

streamlines_native = transform_streamlines(streamlines, np.linalg.inv(affine))
streamlines_actor = actor.line(streamlines_native, fa_img, opacity=0.05)

fig = generate_anatomical_volume_figure(streamlines_actor)
plt.show()

FA Mapped Tractography

Key Points

  • Deterministic tractography methods perform tracking in a predictable way

previous episode

next episode